[This essay, which the The James Clerk Maxwell Foundation site has kindly shared with readers of the Victorian Web, is based on a talk given at the conference
Introduction
It is the hallmark of great physicists that they change our perception of the workings of Nature. These changes in perception are often surprising, even to their originators, go against the perceived wisdom of the time and often encounter considerable resistance to their acceptance. Once however their explanatory power, predictive ability and experimental demonstration become manifest the case for their acceptance becomes overwhelming. The new theories become in their turn the perceived wisdom and future generations wonder why anyone could have doubted their truth and cannot conceive that, at the time the new theories were originated, there were rival theories vying for acceptance.
James Clerk Maxwell and Michael Faraday were great physicists. The truth of the Faraday/Maxwell theory of electromagnetic phenomena, namely that these are described by electric and magnetic fields propagated in space at finite and governed by certain mathematical equations, changed our perception of the world. The theory is now universally accepted and it is forgotten that there were powerful advocates at the time of an alternative theory which I shall call the 'German Theory' of Weber, Neumann, Riemann and Lorenz which was founded on the theory of action at a distance, a physical hypothesis which was entirely alien to the Faraday/Maxwell theory. You will note that I have called the theory, the Faraday/Maxwell theory, rather than just the Maxwell theory. I am sure Maxwell would both have approved and may well have wished this himself as he emphasised the debt which he owed to Faraday. Isaac Newton said "If I have seen further than other men it is because I have stood on the shoulders of giants". Maxwell would have been the first to acknowledge that he stood on the shoulders of Faraday. Indeed Maxwell wrote in his 1864 paper 'A Dynamical Theory of the Electromagnetic Field', which is one of the two or three greatest papers ever written in physics and which set out the famous 'Maxwell Equations' for the first time:
The conception of the propagation of transverse magnetic disturbances to the exclusion of normal ones is distinctly set forth by Professor Faraday in his 'Thoughts on Ray Vibrations'. The electromagnetic theory of light, as proposed by him, is the same in substance as that which I have begun to develop in this paper except that in 1846 there were no data to calculate the velocity of propagation.
The words "as proposed by him" justify calling the "Theory of Electromagnetism" the "Faraday/Maxwell Theory". Because of the universal acceptance of the "Faraday/Maxwell Theory" it is easy to underestimate the boldness of Faraday and Maxwell in putting forward their ideas that electromagnetic disturbances were propagated through a hypothetical aethereal medium — "the aether' whose nature was unknown.
There are well known cases in physics of scientists being extremely reluctant to publish their ideas for fear of incurring the disapprobation of their fellow scholars. One only needs to think of Einstein's initial caution in enunciating his theory that the presence of matter distorts the very geometry of space itself. Einstein published his theory and we have the "General Theory of Relativity" but we cannot leave this brief mention of Einstein without recalling the famous case of the "cosmological constant". Einstein added an extra term, containing the "cosmological constant," to his equations of General Relativity with the sole point and purpose that the equations would allow a steady state universe which he perceived as being the true state of Nature. In his innermost being, he perhaps felt he should have the boldness to omit the term but the expanding universe to which it correctly led was too new (and possibly frightening!) for him to contemplate and he took refuge in the quieter waters of the 'steady state'. When the case for the expanding universe became overwhelming, Einstein called his addition of the cosmological constant "the greatest blunder of my life". In more recent times we may record the initial resistance to Stephen Hawking's suggestion that "black holes," which were previously thought to absorb everything that came within their ambit, were actually bodies that had temperature and entropy and would eventually explode. These instances merely serve to emphasise the boldness of Faraday and Maxwell in putting forward their new theory.
Many commentators have remarked on the contrast between Maxwell's unassuming and rather diffident nature in social contact with people and his bold and imaginative creativity in physics. The explanation may be that the diffidence of Maxwell in social contact only extended to those whom he did not know well - to friends he was the most delightful and charming companion and not averse to voicing unusual or startling views. It is clear that the "Muse of Physics" had been a personal friend of Maxwell from a young age in whose company Maxwell felt no hesitation in expressing his original thoughts.
Place of Clerk Maxwell
Since this conference is devoted to "Scotland's Mathematical Heritage" it is important for Scotland to acknowledge and recognise the proper place for one of its greatest sons. Clerk Maxwell is unquestionably the greatest scientist produced by Scotland but we may legitimately ask the question of where this ranks Maxwell in world terms, since, for example, the greatest composers produced by Scotland may not rank high in world terms. The clear answer, however, is that Maxwell is in the Mozart class right at the very top along with Newton, Einstein, Pasteur, Galileo, Darwin, Copernicus, Lavoisier and Faraday.
The preparation of league tables of great men often encounters academic scorn but since the famous mathematician, G. H. Hardy, used to take delight in ranking cricketers, Trinity men (which Clerk Maxwell was) and even mathematicians in a 'First Eleven' I make no apology for doing so. It seems not unreasonable to rank seven men in the First Division of theoretical physics namely Copernicus in the 15th century, Galileo in the 16th century, Newton in the 17th century, Faraday and Clerk Maxwell in the 19th century and Einstein in the 20th century and perhaps Heisenberg will also be elevated to the same league. I make no apology for ranking Faraday as a theoretical physicist as well as an experimental physicist. As well as conducting wonderful experiments Faraday proposed theories which explained the results. Maxwell himself said "The way in which Faraday himself made use of his idea of lines of force in co-ordinating the phenomena of magnetic-electric induction shows him in reality to have been a mathematician of a very high order". For the word 'mathematician' I think we would substitute the word 'theoretical physicist'.
Each of the great theoretical physicists wrought a revolution and brought a new perception of the physical world as illustrated by the following table.
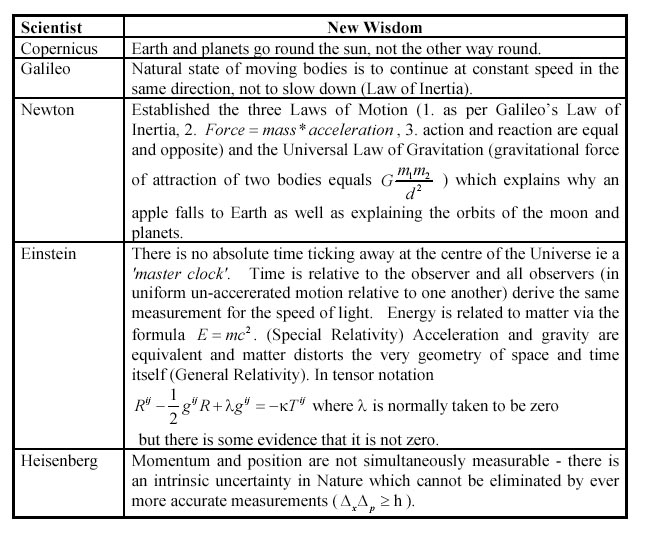
The revolution wrought by Clerk Maxwell and Faraday was that electrical and magnetic phenomenon were best explained, not by a theory founded on instantaneous transmission of forces acting at a distance, but by the propagation of electrical and magnetic fields travelling at the velocity of light. Furthermore they hypothecated that light and radiant heat were manifestations of these electromagnetic waves and that there might be other types of radiation. The truth of the theory is manifest to us each day through radio, television, X-rays, lasers etc.
Maxwell and Faraday if they returned today would surely marvel at the extraordinary diversity of the electromagnetic spectrum and the use to which it has been put in the modern world.
Life and Ancestry
In appreciating one of Scotland's greatest sons it is incumbent on us to know a little more about the man himself than we might know about other scientists of comparable eminence - for example Pasteur. If we learn that Pasteur attended this or that school in France or attended this or that university it may not mean much to us in terms of our own experience or being able to visualise the circumstances of the case. With Clerk Maxwell it is different. We can visualise him walking down from 31 Heriot Row where he stayed with his aunt, Isabella Wedderburn (née Clerk), to the Edinburgh Academy. We can visualise him attending a lecture at this very Royal Society of Edinburgh or listening to the lectures of Sir William Hamilton at Edinburgh University. In the hall of this Royal Society of Edinburgh we can see the original manuscript of Maxwell's paper on a mechanical method of describing "Oval Curves" presented to the Society by Professor Forbes when Maxwell was fourteen. Maxwell's paper 'On the Theory of Rolling Curves' was presented to the Royal Society of Edinburgh when he was eighteen and his paper 'On the Equilibrium of Elastic Solids' was presented when he was nineteen. Thus before Maxwell went to Cambridge he had published three important papers. There is a story told by Professor Thompson, later Master of Trinity College, Cambridge [image of Trinity], as to how Maxwell used these papers to great effect when he wished, after one term at Cambridge, to migrate from Peterhouse College to Trinity College. Maxwell applied to Dr Thompson who was then the Trinity College tutor. At the interview with Dr Thompson, Maxwell appeared to be shy and diffident but presently surprised Dr Thompson by producing a bundle containing three published papers remarking "Perhaps these may show you that I am not unfit to enter at your College." Maxwell was clearly not without confidence in his own intellectual powers.
We are aware that Clerk Maxwell is not as well known in the UK, or even in his home country of Scotland, as he should be. It is also surprising that none of the biographies on Clerk Maxwell remark, to the extent that seems merited, on the astonishing family background of Clerk Maxwell. Clerk Maxwell was, on his father's side, one of the Clerks of Penicuik and on his mother's side a Cay of Northumberland. The Clerk family had produced, in the generations before Clerk Maxwell, men of such conspicuous ability in a wide range of fields that to use the word "genius" is not inappropriate. Indeed Sir Walter Scott himself had praised the "heritable genius" of the Clerk family. It is worth listing the members of the Clerk family and the members of the Cay family who were either Fellows of the Royal Society in London or Fellows of the Royal Society of Edinburgh.

It is rather astonishing to record in the family tree, in the period up to 1882, four Fellows of the Royal Society of London and ten Fellows of the Royal Society of Edinburgh. With a pedigree like that it is perhaps not surprising that Clerk Maxwell was something rather special!
In the course of this short talk I can only whet your appetite by giving a brief glimpse of the remarkable family of Clerks. If you wish to know more may I refer you to a paper in the Bulletin of the Institute of Mathematics and its Applications (Volume 28 Numbers 1/2 January/February 1992).
Sir John Clerk, FRS, FSA, 2nd Baronet, was the great great grandfather of James Clerk Maxwell and was extremely talented - being described by William Stukely, the scholar and antiquary, as the "great genius of the North". His talents covered a vast scope and he was recognised as Scotland's best informed patron of the arts and leader of his generation in the cultural field. He was an antiquarian, architect, historian, poet, scientist, musician, composer, patron, connoisseur, traveller, writer and man of letters, an astonishing range of accomplishments - indeed he was something of a virtuoso in the sense of a man who wishes and will know everything. He helped to found the Philosophical Society in Edinburgh which subsequently became the Royal Society of Edinburgh.
With regard to his musical accomplishments, Sir John was a highly gifted composer and harpsichordist who, during his Grand Tour of Europe, had studied with Corelli in Rome and had very much impressed the latter. Despite the fact that his musical output is small, Sir John Clerk is recognised as one of the finest composers produced by Scotland. John Purser in his book 'Scotland's Music' describes Clerk as follows, "Clerk established himself as a composer well able to handle the musical lingua franca of Europe not just with precocious competence but with a personal conviction and feeling that raises him far above the ordinary". Clerk's works have been performed at the Edinburgh International Festival, at Glasgow Mayfest and on other significant occasions, the most recent being the evening of music, poetry and art titled 'Generations of Genius' held at 14 India Street (Maxwell's birthplace) on 13 June 1995, the 165th anniversary of Maxwell's birth.
Dr. Robert Clerk, the uncle of the Sir John Clerk, FRS, FSA mentioned above, was a prominent Edinburgh surgeon and a member of the Royal College of Surgeons. His son, Dr. John Clerk was a distinguished physician and President of the Royal College of Physicians from 1740-44. He took an active interest in planning, building and management of the Edinburgh Royal Infirmary.
John Clerk of Eldin, FRSE, was the great great uncle of Clerk Maxwell and has a number of claims to fame but among the most remarkable is the book which he wrote entitled 'Essay on Naval Tactics'. This was a scientific critique of naval tactics which advocated the original tactic of 'cutting the line' - that is, to sail directly into the line of the enemy ships and attack the rear ships of that line with the whole force of the attacking fleet. This was the tactic employed successfully by Nelson at Trafalgar. It was extraordinary that Clerk should publish such a book since he was a landsman who had never been to sea but as Professor Playfair, the Professor of Natural Philosophy at Edinburgh University said "The author of Naval Tactics was one of those men who by the force of their own genius have carried great improvements into professions not properly their own". One sees in John Clerk of Eldin a highly original and creative mind of a type later to be revealed in Clerk Maxwell himself.
John Clerk, Lord Eldin, FRSE, the son of John Clerk of Eldin whom I have just described, was the greatest advocate of his day and celebrated for the power of his intellect and the sharpness of his wit. Regarding the sharpness of his wit, I cannot resist telling the following story. Clerk, who had a strong Scottish accent, was pleading a case in the House of Lords before the Lord Chancellor. The case concerned the right to continue using a stream at a mill. As Clerk said "the water had rin that way for forty years, indeed naebody ken't how long, and why should his client be deprived of the water". The Lord Chancellor said in haughty tones "Tell me, Mr Clerk, do you spell the word water with two t's?" Clerk answered "No, My Lord, but you spell the word "manners" with twa n's".
Sir George Clerk, FRS, FRSE, was Maxwell's uncle and had a distinguished political career as a Lord of the Admiralty, Under Secretary of the Home Department, Secretary of the Treasury and Vice President of the Board of Trade. He had considerable interest in science and was, from 1862 to his death in 1867, the President of the Zoological Society at a time when the fierce debate on Darwin's "Theory of Evolution" was raging. No doubt he needed all his political skills to deal with the fierce disputes. It is interesting to note that he was also the Master of the Mint in 1845, a position which Isaac Newton himself had held for 28 years.
Clerk Maxwell's grandfather on his mother's side, that is on the Cay side, was a distinguished lawyer being Judge of the High Court of Admiralty in Edinburgh and a close friend of Sir Walter Scott. There is plenty of evidence of mathematical ability on the Cay side of the family, for example John Cay, FRSE, who was Clerk Maxwell's favourite uncle, was the Sheriff of Linlithgow for some 43 years. It is recorded that he had an enthusiasm for the acquisition of scientific knowledge (he very much liked to attend meetings of the Royal Society of Edinburgh of which he was a member) and although not specially trained in mathematics was extremely skilled in arithmetic and fond of calculation as a voluntary pursuit. William Dyce Cay, FRSE, MICE was James Clerk Maxwell's cousin. He had studied at Edinburgh University where he won the highest mathematical prize, the Straiton Gold Medal, in 1856. William Cay put this down to the excellent tuition he had received from his cousin saying "His [Maxwell's] tuition and example had a good effect as I got the highest prizes in my classes’. Between 1856 and 1858 he served his pupilage in engineering in Belfast with Lord Kelvin's brother, James Thomson, whose ingenuity James Clerk Maxwell has once described as "quite equal to that of his brother.’ In 1872, he was elected a Member of the Institution of Civil Engineers and in 1882 a Fellow of the Royal Society of Edinburgh. Furthermore, Charles Hope Cay, William's brother, was 6th Wrangler in the Cambridge Mathematical Tripos in 1864. In the same year, it was to Charles Hope Cay that Clerk Maxwell wrote, "I also have a paper afloat, with an electromagnetic theory of light, which till I am convinced to the contrary, I hold to be great guns". This is one of the rare occasions in which Clerk Maxwell expressed an opinion about his own work. In 1864, Charles was in his final year at Cambridge and therefore in a position to understand something of the significance of what his cousin was saying. William and Charles Cay together with their sister Elizabeth, a beautiful and highly intelligent girl, were Maxwell's favourite cousins.
Scientific Work
I would now like to turn to Maxwell's scientific work. His collected works contain some 101 scientific papers. If we look however at the major scientific papers which are in excess of 15 pages and leave out the expository articles then we find that there are 16 major papers falling under the following headings:
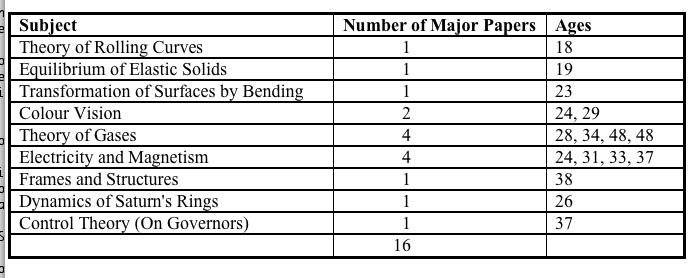
It is interesting to note that Maxwell matured early as a physicist and apart from the two later papers on the Theory of Gases had already published his major works by his late thirties.
I would like to discuss first Maxwell's contribution to electromagnetism.
Theory of Electromagnetism
Clerk Maxwell possessed superb ability to turn physical phenomena into mathematical form. This is clearly seen in his masterly analysis of the stability of Saturn's rings and in his analysis of the statistical behaviour of the molecules in a gas. However the greatest demonstration of this ability is the "Theory of Electromagnetism" because, not only did Maxwell have to turn the experiments which had actually been carried out into mathematical form, he also had to hypothecate the result of an experiment which had not been carried out and which could not be carried out because it was beyond the technical capabilities of scientists in the late 19th century. This is where the creative side of Maxwell's mind is seen to great effect.
It is worth examining the history of electromagnetism to appreciate where Maxwell's contribution fits into the history of the subject. The table below shows the historical development of the subject in the 19th century starting with the battery of Volta just before the start of the 19th century and ending with the first radio signals being sent across the Atlantic by Marconi just after the end of the nineteenth century.
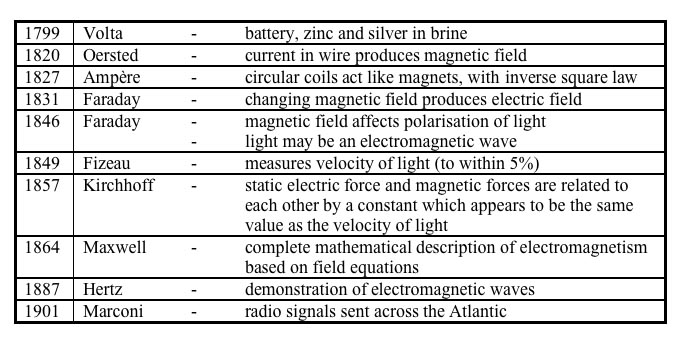
It is worth noting the four papers which Maxwell wrote on electricity and magnetism and recording the age at which he wrote them and the number of pages each contained. The first three papers are well known being the papers which led up to the 1864 paper which exhibited the 'Maxwell Equations' for the first time. Also of interest is the 1868 paper titled 'On a Method of Making a Direct Comparison of Electrostatic with Electromagnetic Force: With a note on the Electromagnetic Theory of Light' - indeed the note on the Electromagnetic Theory of Light is particularly interesting and I shall comment on this later.
Papers on Electricity and Magnetism

We have noted earlier that it was Faraday who originally proposed that light might be an electromagnetic wave but it is interesting to examine the actual wording used by Maxwell in his papers as the theoretical evidence for this mounted. In his 1862 paper, 'On Physical Lines of Force', Maxwell writes:-
The velocity of transverse undulations in our hypothetical medium, calculated from the electromagnetic experiments of Kohlrausch and Weber, agrees so exactly with the velocity of light calculated from the optical experiments of Fizeau that we can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena.
In Maxwell's paper 'A Dynamical Theory of the Electromagnetic Field' of 1864 we find that"The velocity (of the electromagnetic waves) is so nearly that of light that it seems we have strong reason to conclude that light itself (including radiant heat and other radiations if any) is an electromagnetic disturbance in the form of waves propagated through the electromagnetic field according to electromagnetic laws".
It is clear that in 1868, despite Maxwell's earlier papers, the 'German Theory' of electric and magnetic phenomena was still prominent with the 'new' theories of Faraday and Maxwell still struggling for acceptance in the physics community and still far from displacing the 'German Theory'. It seems very likely that this caused Maxwell a certain amount of frustration and in 1868 he set out the four premises on which his electromagnetic theory depended. One may have little doubt that he did this in order to simplify the theory as much as possible and in order that this lucid exposition of the theory would carry conviction among his peers. The four basic premises on which the Electromagnetic Theory depended were set out by Maxwell as follows:-
(i) If a closed curve is drawn embracing an electric current, then the integral of the magnetic intensity taken round the closed curve is equal to the current multiplied by 4* (Oersted/Ampère).
(ii) If a conducting circuit embraces a number of lines of magnetic force and if, from any cause whatever, the number of these lines is diminished, an electromotive force will act round the circuit, the total amount of which will be equal to the decrement of the number of lines of magnetic force in unit of time (Faraday).
(iii) When a dielectric is acted on by an electromotive force it experiences what we call electric polarisation. Within the dielectric there is a displacement of electricity, the displacement being proportional to the electromotive force at each point (Faraday).
(iv) When the electric displacement increases or diminishes the effect is equivalent to that of an electric current (Maxwell).
Maxwell explains premise (iv) in greater detail:
According to this view, the current produced in discharging a condenser is a complete circuit and might be traced within the dielectric itself by a galvanometer properly constructed. I am not aware that this has been done so that this part of the theory, though apparently a natural consequence of the former, has not been verified by direct experiment. The experiment would undoubtedly be a very delicate and difficult one.
Based on these four premises, Maxwell then proceeded to derive the wave equation for the electromagnetic field showing that, on the basis of known fundamental electric and magnetic constants, the velocity of these electromagnetic waves in the hypothetical aethereal medium was equal to that of the known velocity of light as measured by Fizeau.
In the late 1870s it is clear that Maxwell was again somewhat frustrated by the scientific community not giving sufficient attention to comparing the German Theory with the Faraday/Maxwell theory and it may be this that was the motivating force for Maxwell to produce his famous textbook A Treatise on Electricity and Magnetism in 1873. In the introduction to his book Maxwell explains
Great progress has been made in electrical science, chiefly in Germany, by cultivators of the theory of action at a distance. . . . the electromagnetic speculation carried out by Weber, Riemann, J. and C. Neumann, Lorenz etc is founded on the theory of action at a distance. . . . These physical hypotheses however, are entirely alien to the way of looking at things which I adopt. . . . It is exceedingly important that the two methods should be compared . . . . I have therefore taken the part of an advocate rather than that of a judge.
Given that Maxwell was writing his famous book as an advocate of a new theory it is remarkable that his book should stand today almost as a textbook, albeit somewhat old-fashioned, treatment of the subject. Surely only with Newton's Principia can you find another example of a new subject being treated by its originator with an assuredness that has stood the passage of time so remarkably well.
Dynamical Theory of Gases
The table below shows the six papers published by Maxwell on the dynamical theory of gases. The papers are divided into four major papers and two more minor papers. It is interesting that papers 3 and 4 in the Table appeared very nearly at the end of his life, some 13 years after his earlier paper 'On a Dynamical Theory of Gases'.
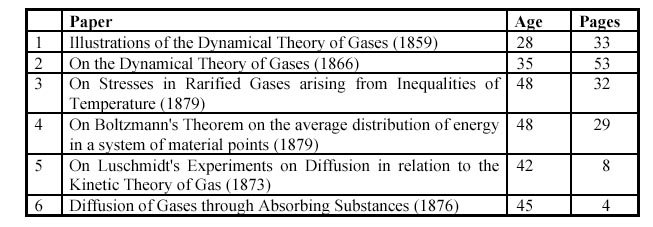
The first paper published by Maxwell assumed that the molecules of a gas were perfectly elastic spheres. On the basis of this assumption Maxwell established the probability distribution for the speed of the molecules — the famous "Maxwell Distribution" — established Boyle's Law, established that if two gases mix freely in a vessel the average kinetic energy of the two types of molecule is equal and showed the rather startling result that the internal friction (viscosity) of a gas was (a) independent of the density of a gas and (b) proportional to the square root of the absolute temperature (but see below). He also established certain rather interesting statistics i.e. that at a temperature of 60’F the average speed of air molecules is 1000 miles per hour, the mean distance between collisions is 2 microns (2 millionth of an inch) and there are 8 billion molecular collisions a second - a somewhat startling figure and rather hard to imagine!
The paper went on to establish that if the molecules were not perfectly elastic spheres but were bodies of any shape then, after a lot of collisions, the average kinetic energy of motion along each of three axes would be the same and equal to the average kinetic energy of rotation about each of the three principal axes of each molecule (Law of Equipartition of Energy).
The paper also pointed out two problems with the theory. The first concerned the specific heat of a gas. There are two specific heats of a gas, namely the specific heat at constant pressure and the specific heat at constant volume. The ratio was known to be 1.408. On the basis of the perfectly elastic sphere model, the spheres having translational energy only, the predicted ratio was 1.667 and on the basis of the molecules being bodies with translational and rotational energy the predicted ratio was 1.333, still well away from the experimental 1.408 although somewhat closer. An elegant experiment by Maxwell established that (a) the viscosity of a gas was indeed independent of density but (b) that the viscosity was proportional to absolute temperature rather than the square root of temperature as stated above. This latter point was the second problem for Maxwell's theory.
In his second paper 'On the Dynamical Theory of Gases' Maxwell modified his theory and assumed that the molecules repelled each other with a force inversely proportional to the fifth power of the distance. This miraculously gave the viscosity of the gas proportional to the absolute temperature! This paper again established the gas laws, and established the law of Dalton regarding mixtures of gases, the law of Graham on diffusion of gases and the law of Gay-Lussac as well as a number of other important results.
The discrepancy over the specific heats was not resolved until quantum theory provided the explanation.
The trigger for Maxwell's third paper 'On Stresses in Rarefied Gases arising from Inequalities in Temperature' was no doubt the radiometer demonstrated by Crookes. In the radiometer a paddle wheel was mounted in an evacuated tube (rarefied gas). The sides of the paddle wheel were painted black and white on opposing sides. The paddle wheel turned indicating that forces were acting in the rarefied gas owing to inequalities of temperature. Maxwell's paper was to elucidate the nature of these forces. The explanation, according to Maxwell, was that the gas in contact with the surface of a solid must slide over it from colder to hotter parts to produce a tangential stress.
His fourth paper, inspired by the work of Boltzmann, took a very generalised approach to the properties of dynamical systems and applied statistical techniques to considering the probability of the system being in a particular state.
Colour Vision
As background to Maxwell's work on colour we may recall various milestones in the investigation of light and colour.
| 1666 | a prism splits light into the colours of the rainbow if experiment reversed, colours combine to white light light is a beam of 'corpuscles' (photons) |
| 1678 | light is a wave |
| 1801 | demonstrated the interference of light calculated the wavelengths of the colours colour stems from three kinds of receptors in the eye sensitive to red, blue, green (tri-chromatic theory) |
Maxwell recognised that experiments in colour had to be judged by what they told us about the eye since colour was essentially the physiological reaction of the eye to the incident wavelengths.
Maxwell's famous colour top and then his colour box confirmed by direct experiment the tri-chromatic theory by producing colour equations. This approach showed for the first time how colours could be linked together quantitatively. For example, the equation below shows how the red, blue and green which Maxwell used could be combined to give white light. The colour top was essentially a spinning top on which were arranged the colours in sectors of a circle, the circumference being divided into 100 units. When the top was spun the colours merged into a third colour. The quantitative measure of colour was the size of the sector occupied by that colour measured by the number of units of the sector at the circumference. This gave rise to equations of the type shown below where the coefficient is the number of units of colour.
37(Red) + 27(Blue) + 36(Green) = 27(White) + 72 (Black)
Using these equations Maxwell showed how other colours could be represented as combinations of three basic colours (in agreement with the trichromatic theory) and plotted on a triangular diagram as suggested by Newton. Maxwell used these techniques to show colour blindness was the absence of sensitivity to a red tint.
Maxwell's famous 1861 coloured projection (on a screen) of a tartan ribbon, which is described, not quite accurately, as the first coloured photograph, stemmed from his attempt to demonstrate the tri-chromatic theory.
I regret that I do not have time to discuss Maxwell's masterly analysis of the dynamical stability of the rings of Saturn, which showed that the rings had to be disconnected particles and not solid or fluid, or his contributions to thermodynamics where the intriguing little creature called Maxwell's Demon first makes an appearance. There is also a set of four equations in thermodynamics known as Maxwell's equations of thermodynamics.
If we add to the papers discussed the papers on framework structures and reciprocal diagrams and the paper on control theory ('On Governors'), which founded the science of cybernetics, we see the extraordinary versatility of Maxwell. Maxwell was indeed 'omni-competent' in physics and it was said that it was almost impossible to mention any aspect of physics, or indeed a published paper, with which Maxwell was not acquainted.
Maxwell the Man
I would like to end by saying something of Maxwell the man. He was modest and unassuming yet possessing a superb intellect, the great capabilities of which he must have recognised himself. He was generous to others and never jealous of their work. There are many instances of his kindness. I shall mention just one. Charles Robertson, fellow Academical and student at the same time as Maxwell at Trinity, had hurt his eyes and was not able to read with any ease. As Charles Robertson wrote later "He [Maxwell] used to find me sitting in my rooms with closed eyes, unable to prepare the next day's lectures, and often gave up an hour of his recreation time to read out to me some of the book-work I wanted to get over".
I cannot end this talk without mentioning Maxwell's superb memory, his acquaintance with the Bible and English literature and his own remarkable powers of versification. At the age of eight he could recite all 176 verses of the 119th Psalm. Throughout his life he would take pleasure in reciting verbatim extensive passages from the Bible and from English literature particularly Shakespeare. The obituary notice of Maxwell published in the Proceedings of the Royal Society recounts that he "was almost as much at home with the students of philosophy and theology as with physics. But if there was one subject more than another in which his conversation was always interesting, it was the literature of his own country, his acquaintance with which, and especially with English poetry, was remarkable alike for its extent, its exactness, and the wide range of his sympathies".
Maxwell's powers as a poet are evident from the verses published in the biography of Maxwell by Lewis Campbell and William Garnett. As Peter Guthrie Tait, the Professor of Natural Philosophy at Edinburgh University said "Maxwell's early skill in versification developed itself in later years into real poetic talent. But it always had an object and often veiled the keenest satire under an air of charming innocence and naive admiration. No living man has shown a greater power of condensing the whole substance of a question into a few clear and compact sentences than Maxwell exhibits in his verses".
On Maxwell's death, the many tributes commented on his independence of mind, native sagacity, honesty of purpose and essential Christian goodness. Scotland has every reason to be proud of this great man and great scientist.
Appendices
1. Books Published By Maxwell
Theory of Heat. 1871.
Treatise on Electricity and Magnetism. 2 Vols. 1873.
Matter and Motion. 1876.
The Electrical Researches of the Hon. Henry Cavendish (1771-81). 1879.
Elementary Treatise on Electricity. 1881 (published after Maxwell's death)
Reports of the Committee on Electrical Standards (Maxwell was a member of the Committee). 1873.
2. Maxwell as Cambridge Examiner
- Mathematical Tripos 1866, 67, 69, 70, 73
- Smith's Prize 1879
- Natural Sciences Tripos 1873, 74
Last modified 24 March 2006